この記事はランク学習(Learning to Rank) Advent Calendar 2018 - Adventarの12本目の記事です
この記事は何?
ニューラルネットを用いたランク学習の手法として、RankNet*1*2という手法が2005年に提案されています。
RankNetの提案自体は10年以上前ですが、シンプルで応用先も広い手法です。
この記事では、PyTorchを用いたRankNetの実装を紹介します。*3
RankNet
"From RankNet to LambdaRank to LambdaMART: An Overview", C. Burges, 2010.の説明に従って紹介します。
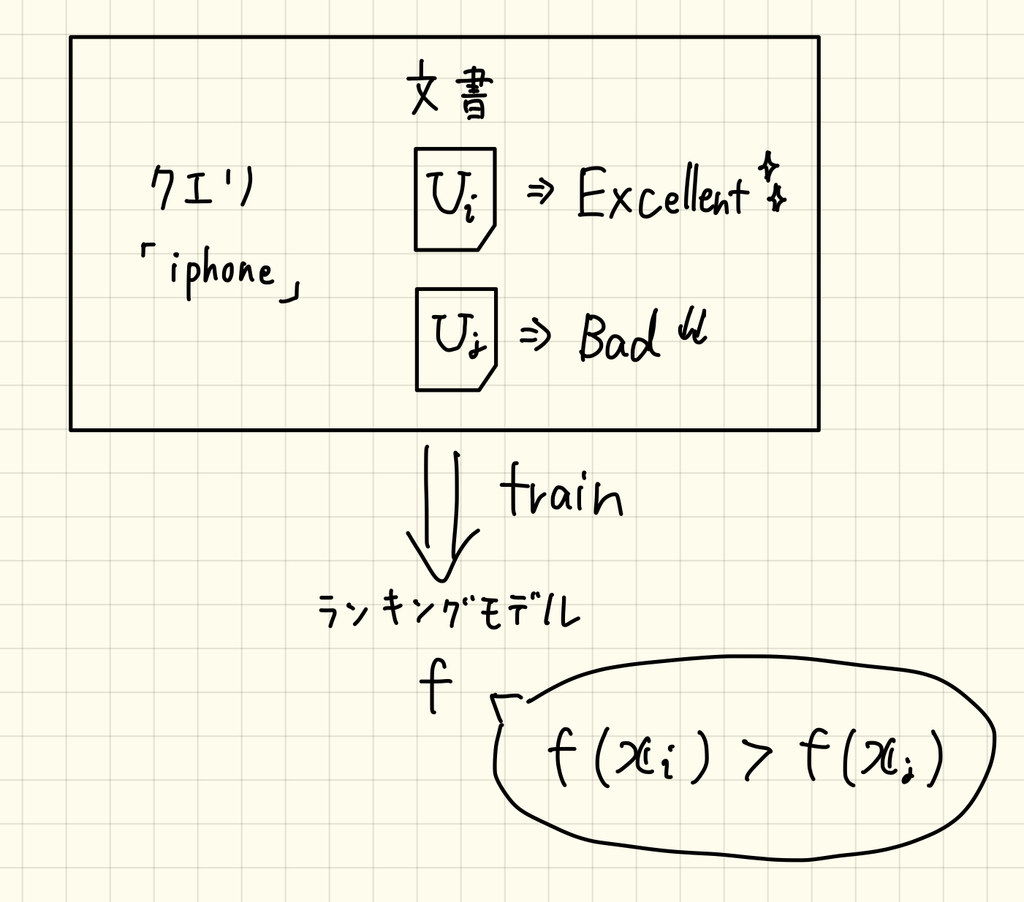
RankNetはランク学習におけるペアワイズ手法に分類されます。
あるクエリについて2つの文書と
が与えられていて、文書
の方が
よりも関連度が高い(
)とき、ランキングモデル
のスコアは文書
の方が高くなるように学習します。
文書と
のスコアをそれぞれ
とします。
この2つのスコアを用いて、となる確率を以下のように定式化します。
上式の気持ちですが
- 文書
のスコア
が非常に大きいケース:ランクモデルは文書
の関連度が高いと言っているときは、
は1に近づくことが分かります。
- 文書
のスコア
が非常に大きいケース:ランクモデルは文書
の関連度が高いと言っているときは、
は0に近づくことが分かります。
上式にはハイパーパラメータとしてが存在しますが、適当なスカラー値が入っていると思っておけば大丈夫です。
さて、手元の学習データから、上式で定義したが真の
に近づくように、ランクモデルを学習させます。
RankNetでは、損失関数として交差エントロピー損失を用いて、学習を行います。
例えばという学習データがあるとき、
となるため、
となり、
をなるべく1に近づけて損失関数を小さくするように学習を行います。
ここで、を以下のように定義します。
すると、真の確率はと表せ、損失関数を下のように書き換えることができます。
というわけで、損失関数が定義できたので、あとはこれを最適化していけばOKです!
PyTorchを用いたRankNetの実装
それでは、本題のPyTorchを用いたRankNetの実装を紹介します。
まずはネットワークの定義です。
今回は単純なfeed-forwardニューラルネットワークを使います。
class Net(nn.Module): def __init__(self, D): super(Net, self).__init__() self.l1 = nn.Linear(D, 10) self.l2 = nn.Linear(10, 1) def forward(self, x): x = torch.sigmoid(self.l1(x)) x = self.l2(x) return x
さて、本実装のメインとなるRankNetにおける損失関数の定義です。
def pairwise_loss(s_i, s_j, S_ij, sigma=1): C = torch.log1p(torch.exp(-sigma * (s_i - s_j))) if S_ij == -1: C += sigma * (s_i - s_j) elif S_ij == 0: C += 0.5 * sigma * (s_i - s_j) elif S_ij == 1: pass else: raise ValueError("S_ij: -1/0/1") return C
は、上で紹介したRankNetの手法と対応しています。
この損失関数の実装は複数入力(ベクトル)を取れない形になっているので、お好みで拡張してください。
ネットワークと損失関数を定義できたので、実際に動かしてみます。
実験のためにトイデータセットを作ります。
def make_dataset(N_train, N_valid, D): ws = torch.randn(D, 1) X_train = torch.randn(N_train, D, requires_grad=True) X_valid = torch.randn(N_valid, D, requires_grad=True) ys_train_score = torch.mm(X_train, ws) ys_valid_score = torch.mm(X_valid, ws) bins = [-2, -1, 0, 1] # 5 relevances ys_train_rel = torch.Tensor( np.digitize(ys_train_score.clone().detach().numpy(), bins=bins) ) ys_valid_rel = torch.Tensor( np.digitize(ys_valid_score.clone().detach().numpy(), bins=bins) ) return X_train, X_valid, ys_train_rel, ys_valid_rel
今回は各文書に5段階評価のラベルが付与されているものとします。
本当は、ランク学習ではクエリID(qid)と紐づくようなデータセットが用いられますが、今回は簡単のためクエリIDについては無視しています。
精度評価は簡単のため、真の順序と予測の順序がひっくり返ってしまった数(swapped-pairs)を用います。
swapped-pairsが小さいと、予測精度が高いことを表します。
def swapped_pairs(ys_pred, ys_target): N = ys_target.shape[0] swapped = 0 for i in range(N - 1): for j in range(i + 1, N): if ys_target[i] < ys_target[j]: if ys_pred[i] > ys_pred[j]: swapped += 1 elif ys_target[i] > ys_target[j]: if ys_pred[i] < ys_pred[j]: swapped += 1 return swapped
学習・精度評価を合わせたソースコードの全体像を公開しておきます。*4
github.com
上のコードを実行すると、epoch毎にvalidationデータにおけるswapped-pairsを出力します。
epoch: 1 valid swapped pairs: 1735/4950 epoch: 2 valid swapped pairs: 1194/4950 epoch: 3 valid swapped pairs: 885/4950 epoch: 4 valid swapped pairs: 589/4950 epoch: 5 valid swapped pairs: 453/4950 epoch: 6 valid swapped pairs: 350/4950 epoch: 7 valid swapped pairs: 295/4950 epoch: 8 valid swapped pairs: 249/4950 epoch: 9 valid swapped pairs: 226/4950 epoch: 10 valid swapped pairs: 204/4950
学習が進むにつれて、swapped-pairsの数が小さくなっていくことが分かります!
まとめ
この記事ではPyTorchを用いたRankNetの実装を紹介しました。
今回は簡単なネットワークで実装しましたが、もっと複雑なネットワーク(入力クエリと文書の単語から得られるembedding vectorを入力にするなど)も考えられます。
注意ですが、今回の実装は計算効率は特に考えていないので、そのまま使うと速度面で問題があるかもしれません。。。