この記事はランク学習(Learning to Rank) Advent Calendar 2018 - Adventarの6本目の記事です。
この記事は何?
ランク学習の手法は数え切れないくらい提案されていますが、2018年現在のランク学習研究でもbaselineとして使われている手法として、RankSVMがあります。
RankSVMはSVMをランク学習に応用した手法であり、ペアワイズ手法の1つとなります。
次の記事で取り上げますが、RankSVMはお手軽に実行できるツールがあるため、とりあえずランク学習をやってみたいというケースでもオススメです。
この記事では、RankSVMの気持ちをざっくりと紹介します。
SVMの復習
RankSVMを理解する前に、まずはSVMの復習をします。
SVMでは、正例と負例がどのくらい離れているか=マージンがなるべく大きくなるような分類境界を求めます。
PRMLで使われている図が分かりやすいと思います。
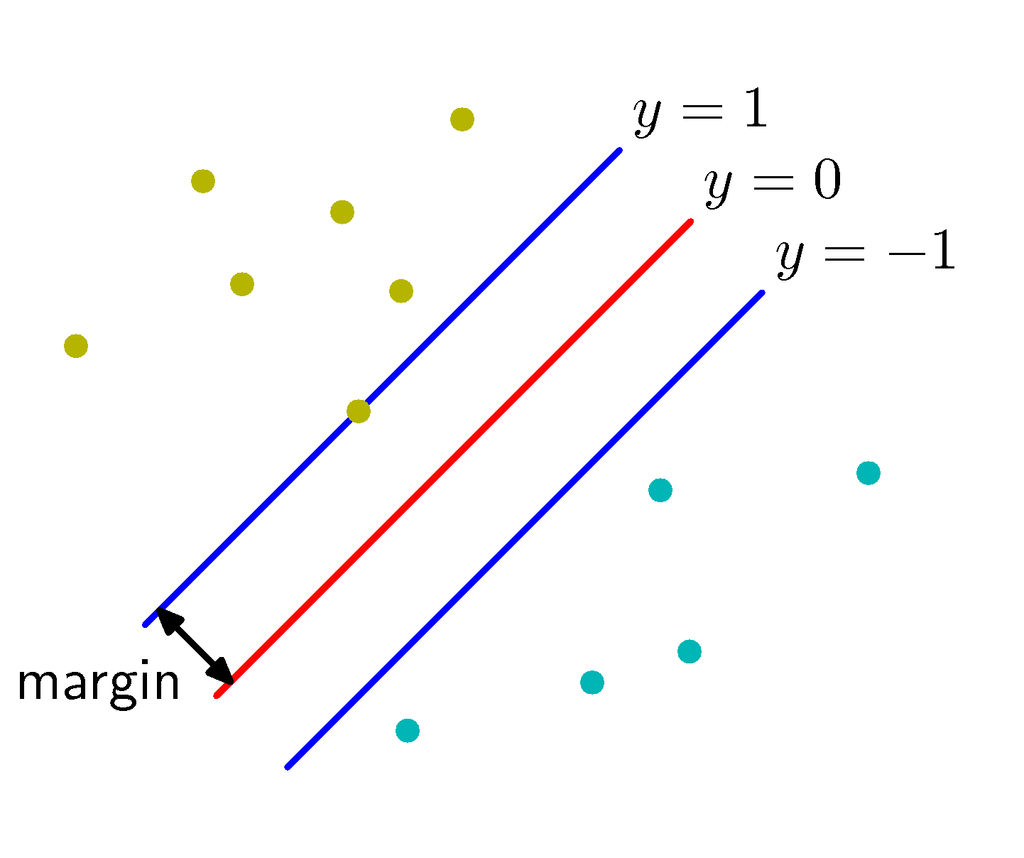
"Pattern Recognition and Machine Learning", C. Bishop, Fig 7.1a
後でRankSVMの目的関数を紹介しますが、比較のために線形SVMの目的関数を取り上げます。
上式は様々な文献で紹介されているので、導出などはそちらを参考にしてください。
私は、機械学習プロフェッショナルシリーズから出ているサポートベクトルマシン本が分かりやすくて好きです。
www.kspub.co.jp
RankSVMを絵で理解する
SVMは正例と負例のマージンを最大化するように学習しました。
RankSVMでも同じようにマージンの考え方が存在します。
"Ranking Support Vector Machine with Kernel Approximation", K. Chen, 2017の図が非常に分かりやすいです。
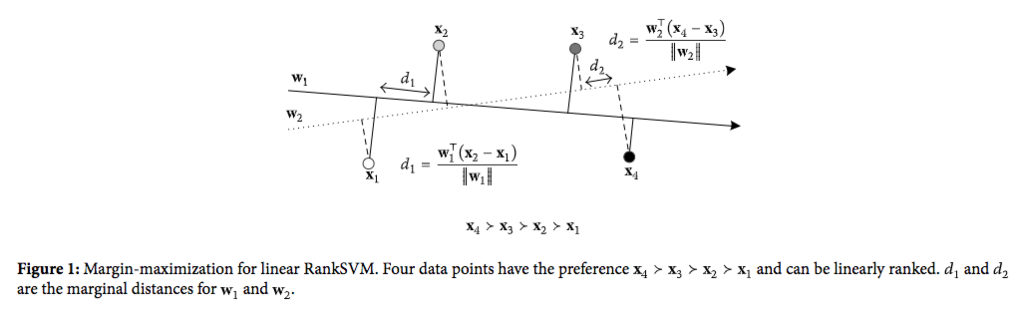
"Ranking Support Vector Machine with Kernel Approximation", K. Chen, 2017. Figure 1.
上の図をじっくり見ていきます。
まず、データ点はの4つがあり、それぞれ2次元の特徴量で表されています。
ランク学習で用いられるデータ点にはそれぞれ関連度を表すラベルが付与されており、よく「Perfect(4)・Excellent(3)・Good(2)・Fair(1)・Bad(0)」などの5段階評価ラベルが使われます。
上の図では、関連度ラベルに従って、という順序関係が与えられています。
さて、RankSVMにおけるマージン最大化の考え方ですが、「全ての順序ペアに関するランキングスコアの差のうち、最小のランキングスコアの差(マージン)を最大化する」というアイデアでパラメータを学習します。
…何言ってんのって感じだと思うので、再度上の図に戻ります。
上の図では2つのパラメータ(重みベクトル)があり、それぞれデータ点の特徴量との内積を取ることでランキングスコアを求めることができます。
を用いた場合は、全ての順序ペアに関するランキングスコアの差のうち、最小のランキングスコアの差は、
と
の間で計算される
となります。
を用いた場合は、全ての順序ペアに関するランキングスコアの差のうち、最小のランキングスコアの差は、
と
の間で計算される
となります。
ここで、と
の大きさを比較すると、
の方が大きいので、パラメータ
によるランキングモデルの方がマージンが大きい(汎化性能が優れている)と言えます。
線形RankSVMの目的関数
RankSVMを絵で理解できたところで、線形RankSVMの目的関数を紹介します。
RankSVMの元論文である"Optimizing Search Engines using Clickthrough Data", T. Joachims, 2002.では、以下のように線形RankSVMの目的関数を定義しています。
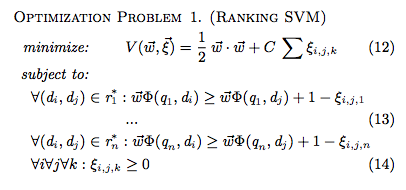
上式ですが、個の検索キーワードに対する検索結果(学習サンプル)のランキングが
として与えられています。
それぞれのランキングから関連度に従って得られた文書対から、制約の式が与えられています。
SVMの目的関数を見てからRankSVMの目的関数を見ると、なんとなくやりたいことが見えてくるんじゃないかなと思います。*1
まとめ
この記事ではRankSVMの気持ちをざっくりと紹介してみました。次の記事ではSVM-rankというRankSVMを実行するツールを紹介したいと思います。
*1:ソフトマージンの式にはなっていますが。