この記事は何?
ランク学習は様々な手法が提案されていますが、勾配ブースティング木を用いたランク学習手法であるGBrankがZ. Zhengら(2007)によって提案されています。
今回はGBrankを1から実装したので紹介したいと思います。
結果だけ見たい方は記事下の方から先にご覧ください。
GBrankのアルゴリズム
アルゴリズムの導出は元論文を読んでいただくとして、アルゴリズムの流れを説明します。
元論文で説明されているアルゴリズムを以下に示します。

明示されていませんが、ハイパーパラメータとしておよび木の数を指定する必要があります。
まず、アルゴリズム初期化部分の"Start with an initial guess "ですが、
は勾配ブースティング木の初期状態における予測を表します。
後で実装を紹介しますが、今回はをどんな値についても0と予測する回帰木を用いました。
次に、アルゴリズム(1)の"we separate into two disjoint sets"について説明します。
訓練データについて、
に対応するラベルが
に対応するラベルよりも強い(e.g. "Excellent"は"Good"よりも強い)とき、
とします。
また、訓練データ中の順序関係にあるペアの集合をとします。
アルゴリズム(1)では前段までの予測を用いてを2つの集合
に分割します。
ちなみに、実装で必要なのはだけです。
続いてアルゴリズム(2)ですが、(1)で求めたを用いて
本目の回帰木
を学習します。
最後にアルゴリズム(3)ですが、前段までの予測およびアルゴリズム(2)で求めた
本目の回帰木
を合わせて、
段目の予測
を求めます。
GBrankの実装
GBrankを実装するにあたって、次の2つを実装する必要があります。
- 回帰木
- GBrankにおける勾配ブースティングの学習
まずは回帰木を実装しましょう。
回帰木の実装
回帰木ですが、最初1つの根ノードから始めて、最小二乗誤差が小さくなるように分割を繰り返していけば実装できます。
The Elements of Statistical Learning(カステラ本)が参考になると思います。
今回は、過学習を防ぐために葉に割り当てられる最小データ数を設定するようにしました。
以下Pythonによる実装です。
※注意:以下のコードはオラオラっと書いたまま最適化していないので、効率の悪い実装だと思います。scikit-learnの実装とかを参考にするべきだと思います。
import numpy as np class Node(object): def __init__(self, parent, data_index, predict_value): self.parent = parent self.data_index = data_index self.predict_value = predict_value self.left = None self.right = None self.split_feature_index = None self.split_feature_value = None class RegressionTree(object): def __init__(self, min_data_in_leaf): self.min_data_in_leaf = min_data_in_leaf self.tree = None def fit(self, X, ys): tree = Node(None, np.arange(X.shape[0]), np.mean(ys)) cand_leaves = [tree] while len(cand_leaves) != 0: # 分割すべき葉を求める min_squared_error = np.inf for leaf in cand_leaves: X_target = X[leaf.data_index] ys_target = ys[leaf.data_index] # どの特徴量で分割するかを決める for d in range(X_target.shape[1]): # d番目の特徴量でデータを並び替える argsort = np.argsort(X_target[:, d]) # 二乗誤差が最小となる分割を求める for split in range(1, argsort.shape[0]): # [0, split), [split, N_target)で分割 tmp_left_data_index = argsort[:split] tmp_right_data_index = argsort[split:] left_predict = np.mean(ys_target[tmp_left_data_index]) left_squared_error = np.sum((ys_target[tmp_left_data_index] - left_predict) ** 2) right_predict = np.mean(ys_target[tmp_right_data_index]) right_squared_error = np.sum((ys_target[tmp_right_data_index] - right_predict) ** 2) squared_error = left_squared_error + right_squared_error if squared_error < min_squared_error: min_squared_error = squared_error target_leaf = leaf left_data_index = leaf.data_index[tmp_left_data_index] right_data_index = leaf.data_index[tmp_right_data_index] split_feature_index = d split_feature_value = X_target[:, d][tmp_right_data_index[0]] # 分割する葉が求まらないときは終了 if min_squared_error == np.inf: break # 分割する葉を候補集合から取り除く cand_leaves.remove(target_leaf) # 分割後の子ノードに割り当てられる要素数がmin_data_in_leaf未満なら, その葉では分割しない if left_data_index.shape[0] < self.min_data_in_leaf or right_data_index.shape[0] < self.min_data_in_leaf: continue # target_leafで分割を行う left_node = Node(target_leaf, np.sort(left_data_index), np.mean(ys[left_data_index])) right_node = Node(target_leaf, np.sort(right_data_index), np.mean(ys[right_data_index])) target_leaf.split_feature_index = split_feature_index target_leaf.split_feature_value = split_feature_value target_leaf.left = left_node target_leaf.right = right_node # 新しい葉を分割候補の葉リストに追加 if left_node.data_index.shape[0] > 1: cand_leaves.append(left_node) if right_node.data_index.shape[0] > 1: cand_leaves.append(right_node) self.tree = tree def predict(self, X): ys_predict = [] for xs in X: node = self.tree # 葉に到達するまで移動 while node.left is not None and node.right is not None: if xs[node.split_feature_index] < node.split_feature_value: node = node.left else: node = node.right ys_predict.append(node.predict_value) return np.array(ys_predict)
GBrankにおける勾配ブースティングの学習の実装
上で紹介したGBrankのアルゴリズムに従って、GBrankを実装していきます。
from itertools import combinations import numpy as np from regression_tree import RegressionTree class GBrank(object): def __init__(self, n_trees, min_data_in_leaf, sampling_rate, shrinkage, tau=0.5): self.n_trees = n_trees self.min_data_in_leaf = min_data_in_leaf self.sampling_rate = sampling_rate self.shrinkage = shrinkage self.tau = tau self.trees = [] def fit(self, X, ys, qid_lst): for n_tree in range(self.n_trees): # 最初の木は0を返すだけの木とする if n_tree == 0: # X = [[0]], ys = [0] を学習させれば0を返す木となる rt = RegressionTree(1) rt.fit(np.array([[0]]), np.array([0])) self.trees.append(rt) continue target_index = np.random.choice( X.shape[0], int(X.shape[0] * self.sampling_rate), replace=False ) X_target = X[target_index] ys_target = ys[target_index] qid_target = qid_lst[target_index] # 直前の木々で予測を行う ys_predict = self._predict(X_target, n_tree) # 出現するqid qid_target_distinct = np.unique(qid_target) # 各qidに対応する訓練データを取得し, n_tree本目の木で学習する訓練データを生成する X_train_for_n_tree = [] ys_train_for_n_tree = [] for qid in qid_target_distinct: X_target_in_qid = X_target[qid_target == qid] ys_target_in_qid = ys_target[qid_target == qid] ys_predict_in_qid = ys_predict[qid_target == qid] for left, right in combinations(enumerate(zip(ys_target_in_qid, ys_predict_in_qid)), 2): ind_1, (ys_target_1, ys_predict_1) = left ind_2, (ys_target_2, ys_predict_2) = right # (ys_target_1 > ys_target_2)となるように交換 if ys_target_1 < ys_target_2: ys_target_1, ys_target_2 = ys_target_2, ys_target_1 ys_predict_1, ys_predict_2 = ys_predict_2, ys_predict_1 ind_1, ind_2 = ind_2, ind_1 if ys_predict_1 < ys_predict_2 + self.tau: X_train_for_n_tree.append(X_target_in_qid[ind_1]) ys_train_for_n_tree.append(ys_target_in_qid[ind_1] + self.tau) X_train_for_n_tree.append(X_target_in_qid[ind_2]) ys_train_for_n_tree.append(ys_target_in_qid[ind_2] - self.tau) X_train_for_n_tree = np.array(X_train_for_n_tree) ys_train_for_n_tree = np.array(ys_train_for_n_tree) # n_tree本目の木を学習 rt = RegressionTree(self.min_data_in_leaf) rt.fit(X_train_for_n_tree, ys_train_for_n_tree) self.trees.append(rt) def _predict(self, X, n_predict_trees): # n_predict_trees本の木による予測結果リストを求める predict_lst_by_trees = [self.trees[n_tree].predict(X) for n_tree in range(n_predict_trees)] # 各木による予測を統合する predict_result = predict_lst_by_trees[0] for n_tree in range(1, n_predict_trees): predict_result = (n_tree * predict_result + self.shrinkage * predict_lst_by_trees[n_tree]) / (n_tree + 1) return predict_result def predict(self, X): return self._predict(X, len(self.trees))
学習の際にqid(各データが紐づくID)を指定するようにしました。詳しくはSVM-rankの入力となるsvmlight形式などを参考にしてください。
また、sampling_rateを設定できるようにしました。
はノリで0.5としました、どれくらいの値がいいのかよくわかってないです。
実装の確認・実験
回帰木およびGBrankの実装の確認をします。
回帰木の実装の確認
scikit-learnにある回帰問題生成関数のmake_regressionを使って訓練データを生成し、上で実装した回帰木で学習した後、訓練データをそのまま入力として出力を確認します。
せっかくなので、graphvizを使って木自体の構造も出力しました。
from queue import Queue import numpy as np import matplotlib.pyplot as plt from graphviz import Digraph from sklearn.datasets import make_regression from regression_tree import RegressionTree def draw_tree(regression_tree, filename): # graphvizで木構造を出力する G = Digraph(format="png") que = Queue() que.put((regression_tree.tree, 0)) while not que.empty(): top, node_num = que.get() # leaf node if top.split_feature_index is None: G.node(str(node_num), "{0:.3f}".format(top.predict_value), shape="doublecircle") # internal node else: G.node(str(node_num), "{0}:{1:.3f}".format(top.split_feature_index, top.split_feature_value), shape="circle") # 2分木なので, 子ノード番号は(親ノード番号 * 2 + 1, 親ノード番号 * 2 + 2)とする if top.left is not None: G.edge(str(node_num), str(node_num * 2 + 1), label="<") que.put((top.left, node_num * 2 + 1)) if top.right is not None: G.edge(str(node_num), str(node_num * 2 + 2), label=">=") que.put((top.right, node_num * 2 + 2)) G.render(filename) if __name__ == '__main__': rt_1 = RegressionTree(1) rt_3 = RegressionTree(3) rt_5 = RegressionTree(5) N = 20 D = 1 X, ys = make_regression(n_samples=N, n_features=D, random_state=0, noise=4.0, bias=100.0) rt_1.fit(X, ys) rt_3.fit(X, ys) rt_5.fit(X, ys) draw_tree(rt_1, "rt_1") draw_tree(rt_3, "rt_3") draw_tree(rt_5, "rt_5") X_test = np.linspace(X.min(), X.max(), 1000).reshape(-1, 1) ys_predict_1 = rt_1.predict(X_test) ys_predict_3 = rt_3.predict(X_test) ys_predict_5 = rt_5.predict(X_test) plt.scatter(X, ys, color="black", label="true") plt.plot(X_test, ys_predict_1, color="red", label="min_data_in_leaf=1") plt.plot(X_test, ys_predict_3, color="green", label="min_data_in_leaf=3") plt.plot(X_test, ys_predict_5, color="blue", label="min_data_in_leaf=5") plt.legend() plt.savefig("fig_test_regression_tree.png")
葉に割り当てられる最小データ数を1, 3, 5と変えて学習してみました。
まずは正しく学習できているかを確認します。
以下の図のx軸は入力変数(今回は1次元の入力です)、y軸は出力変数を表します。
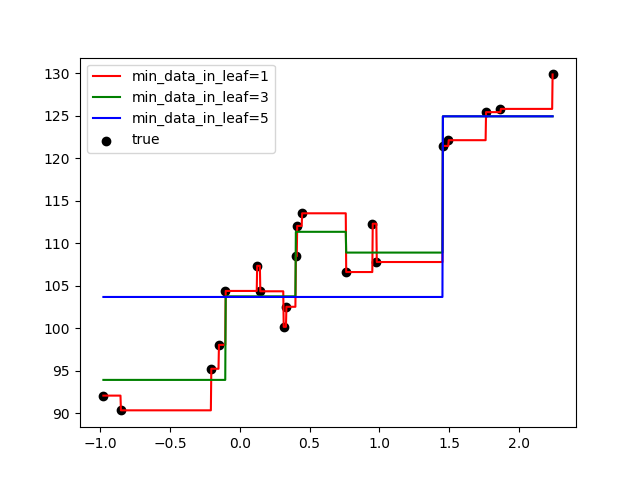
葉に割り当てられる最小データ数を1とすると過学習(学習データに絶対合わせる)しており、最小データ数を5とすると全然当てはまってないことが分かります。
葉に割り当てられる最小データ数が1の時の木構造を見てみます。
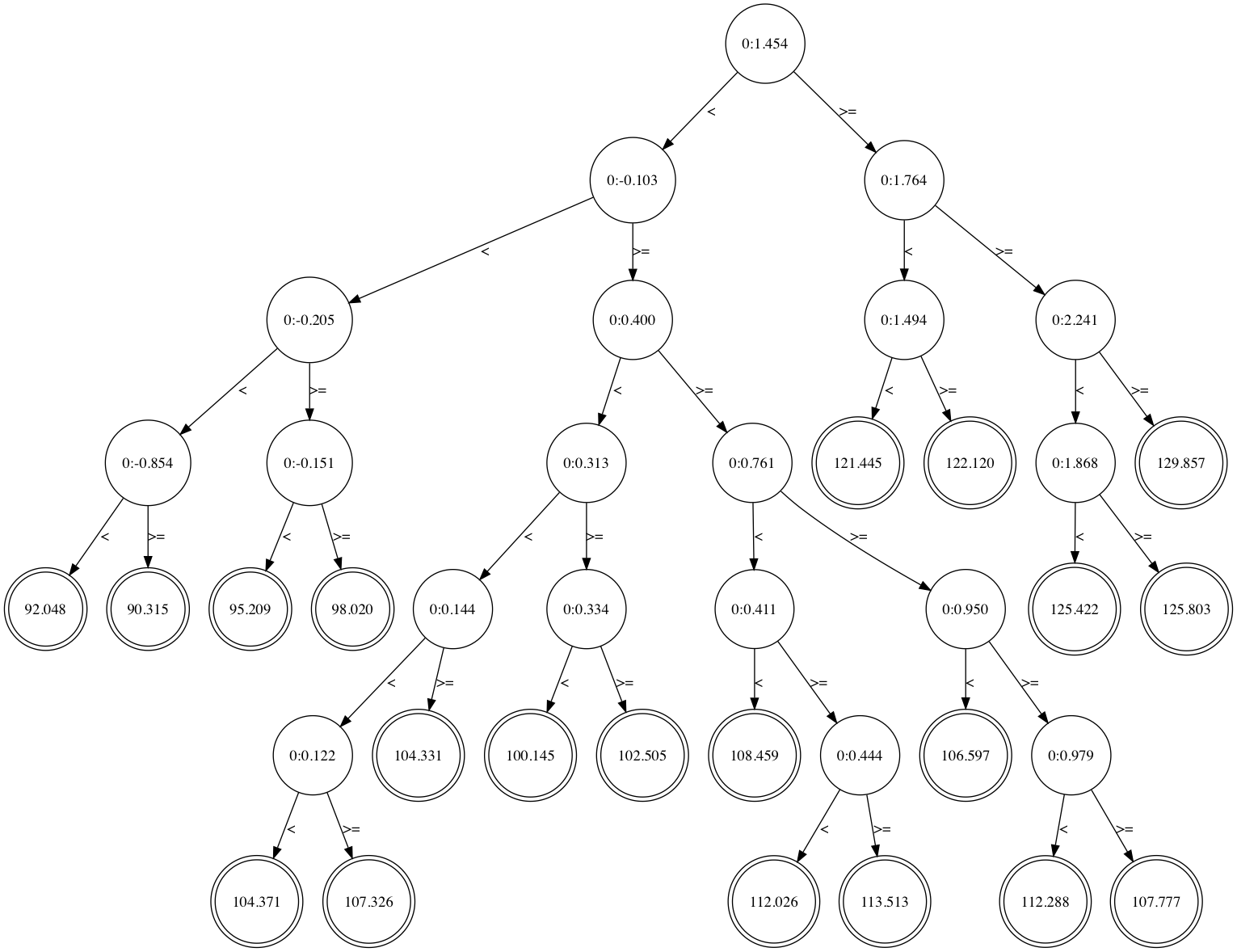
絶対に訓練データに合わせてやろうという気概が見えます。
葉に割り当てられる最小データ数が5の時の木構造も見てみます。
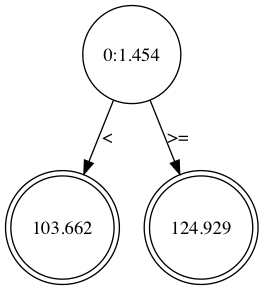
全くやる気が見られないですね。
GBrankの実装の確認
本題のGBrankの実装を確認します。
入力データとしてSVM-rank: Support Vector Machine for Rankingで使われている簡単なデータセットを用います。
3 qid:1 1:1 2:1 3:0 4:0.2 5:0 # 1A 2 qid:1 1:0 2:0 3:1 4:0.1 5:1 # 1B 1 qid:1 1:0 2:1 3:0 4:0.4 5:0 # 1C 1 qid:1 1:0 2:0 3:1 4:0.3 5:0 # 1D 1 qid:2 1:0 2:0 3:1 4:0.2 5:0 # 2A 2 qid:2 1:1 2:0 3:1 4:0.4 5:0 # 2B 1 qid:2 1:0 2:0 3:1 4:0.1 5:0 # 2C 1 qid:2 1:0 2:0 3:1 4:0.2 5:0 # 2D 2 qid:3 1:0 2:0 3:1 4:0.1 5:1 # 3A 3 qid:3 1:1 2:1 3:0 4:0.3 5:0 # 3B 4 qid:3 1:1 2:0 3:0 4:0.4 5:1 # 3C 1 qid:3 1:0 2:1 3:1 4:0.5 5:0 # 3D
1列目は各データの関連度(4が一番強くて1が一番弱い)を、2列目のqidは各データの紐づくグループのIDを、3列目以降は特徴ベクトルを表します。
各データの順序関係は以下の通りです。
1A>1B, 1A>1C, 1A>1D, 1B>1C, 1B>1D 2B>2A, 2B>2C, 2B>2D 3C>3A, 3C>3B, 3C>3D, 3B>3A, 3B>3D, 3A>3D
異なるqid間では比較不可能なことに注意です。
それでは、上で実装したGBrankを動かしてみます。
from itertools import combinations import numpy as np from gbrank import GBrank def show_order(comments, ys, qid_lst): # ysに従った順序関係を示す qid_distinct = np.unique(qid_lst) for qid in qid_distinct: order_strs = [] comments_in_qid = comments[qid_lst == qid] ys_in_qid = ys[qid_lst == qid] for left, right in combinations(zip(comments_in_qid, ys_in_qid), 2): if left[1] > right[1]: order_strs.append("{} > {}".format(left[0], right[0])) elif left[1] < right[1]: order_strs.append("{} > {}".format(right[0], left[0])) print(", ".join(order_strs)) if __name__ == '__main__': train_dat = ( "3 qid:1 1:1 2:1 3:0 4:0.2 5:0 # 1A\n" "2 qid:1 1:0 2:0 3:1 4:0.1 5:1 # 1B\n" "1 qid:1 1:0 2:1 3:0 4:0.4 5:0 # 1C\n" "1 qid:1 1:0 2:0 3:1 4:0.3 5:0 # 1D\n" "1 qid:2 1:0 2:0 3:1 4:0.2 5:0 # 2A\n" "2 qid:2 1:1 2:0 3:1 4:0.4 5:0 # 2B\n" "1 qid:2 1:0 2:0 3:1 4:0.1 5:0 # 2C\n" "1 qid:2 1:0 2:0 3:1 4:0.2 5:0 # 2D\n" "2 qid:3 1:0 2:0 3:1 4:0.1 5:1 # 3A\n" "3 qid:3 1:1 2:1 3:0 4:0.3 5:0 # 3B\n" "4 qid:3 1:1 2:0 3:0 4:0.4 5:1 # 3C\n" "1 qid:3 1:0 2:1 3:1 4:0.5 5:0 # 3D" ) # train_dat読み込み X = [] ys = [] qid_lst = [] comments = [] for line in train_dat.split("\n"): elems = line.split(" ") ys.append(int(elems[0])) qid_lst.append(int(elems[1].split(":")[1])) xs = [] for i in range(5): xs.append(float(elems[2 + i].split(":")[1])) X.append(xs) comments.append(elems[-1]) X = np.array(X) ys = np.array(ys) qid_lst = np.array(qid_lst) comments = np.array(comments) n_trees = 20 min_data_in_leaf = 2 sampling_rate = 0.8 shrinkage = 0.1 np.random.seed(0) gbrank = GBrank(n_trees, min_data_in_leaf, sampling_rate, shrinkage) gbrank.fit(X, ys, qid_lst) ys_predict = gbrank.predict(X) print("correct order") show_order(comments, ys, qid_lst) print("\npredicted order") show_order(comments, ys_predict, qid_lst)
実行すると、以下の結果が得られます。
correct order 1A > 1B, 1A > 1C, 1A > 1D, 1B > 1C, 1B > 1D 2B > 2A, 2B > 2C, 2B > 2D 3B > 3A, 3C > 3A, 3A > 3D, 3C > 3B, 3B > 3D, 3C > 3D predicted order 1A > 1B, 1A > 1C, 1A > 1D, 1B > 1C, 1B > 1D, 1C > 1D 2B > 2A, 2C > 2A, 2B > 2C, 2B > 2D, 2C > 2D 3B > 3A, 3C > 3A, 3A > 3D, 3C > 3B, 3B > 3D, 3C > 3D
GBrankの出力自体は実数値なので、例えば2Aと2Cのように関連度が同じ入力だとしても予測では順序関係を与えてしまいます。
そのため、正しい順序関係が予測された順序関係に内包されていれば、正しく予測ができていると言えます。
その他
勾配ブースティング木を用いたランク学習手法として、今回挙げたGBrank以外にもLambdaMARTがあります。
そのうち実装したいですね。。。
ぶっちゃけGBrankの実装よりも回帰木の実装の方がめんどい。。。